Skip to main content

차원 축소

다차원 데이터를 보다 낮은 차원 공간으로 매핑하는 노드입니다.

설명​

차원 축소 노드는 고차원 데이터를 저차원으로 변환합니다.

PCA 또는 t-SNE 알고리즘을 선택할 수 있으며, 데이터의 주요 특성을 유지하면서 차원을 줄여 시각화 및 분석을 용이하게 합니다.

포트 구성​

입력 포트​

  • 데이터셋

출력 포트​

  • 데이터셋: 고차원의 구조를 고려한 저차원의 데이터셋(Feature가 축소됨)

속성​

사용하지 않을 열 선택​

차원 축소에서 고려하지 않을 열을 선택합니다.

선택한 열은 차원 축소 계산에서 제외됩니다.

차원 축소 방법 선택​

차원 축소 방법을 선택합니다:

  • PCA (Principal Component Analysis): 주성분 분석을 통해 데이터의 분산을 최대한 보존하면서 차원을 축소합니다
  • t-SNE (t-Distributed Stochastic Neighbor Embedding): 고차원 데이터의 지역적 구조를 보존하면서 저차원으로 매핑합니다

출력 차원​

출력할 차원의 수를 정합니다.

출력할 차원의 수는 입력한 차원의 수 이하이어야 합니다.

복잡도(Perplexity) - t-SNE 선택 시​

t-SNE 알고리즘에서 데이터의 지역적 구조를 반영하는 파라미터입니다.

복잡도는 t-SNE가 임베딩 과정에서 각 데이터 포인트의 '이웃'을 얼마나 많이 고려할지를 결정합니다:

  • 낮은 복잡도: 근처 이웃만 고려하여 데이터의 지역적인 구조를 잘 반영하지만, 전반적인 구조 파악에는 적합하지 않을 수 있습니다
  • 높은 복잡도: 더 많은 이웃을 고려해서 데이터의 전반적인 구조를 잘 반영하지만, 세밀한 지역적 구조를 놓칠 수 있습니다

거리 측정 방법 - t-SNE 선택 시​

벡터 공간 내 데이터 포인트 사이의 거리 측정 방법을 선택합니다.

두 데이터 포인트의 거리가 가까울수록 두 점의 특징(feature)이 유사할 가능성이 높습니다:

  • 유클리드 거리(Euclidean Distance): 두 점 사이의 직선 거리
dij=∣∣xi−xj∣∣=∑k=1D(xik−xjk)2d_{ij} = ||x_i - x_j|| = \sqrt{\sum_{k=1}^{D}(x_{ik} - x_{jk})^2}

D는 데이터의 차원 수를 나타내고, xikx_{ik}와 xjkx_{jk}는 각각 데이터 포인트 xix_i와 xjx_j의 k번째 차원 값을 의미합니다.

  • 맨하탄 거리(Manhattan Distance): 두 데이터 포인트 사이의 절대적 좌표 차이의 합
d(x,y)=∑i=1n∣xi−yi∣d(x, y) = \sum_{i=1}^{n}|x_i - y_i|

n차원 공간에서의 두 점 x=(x1,x2,...,xn)x = (x_1, x_2, ..., x_n)와 y=(y1,y2,...,yn)y = (y_1, y_2, ..., y_n) 사이의 맨하탄 거리입니다.

  • 코사인 유사도(Cosine Similarity): 두 벡터 간의 각도를 이용한 유사도 측정
A⋅B∣∣A∣∣∣∣B∣∣=∑i=1nAiBi∑i=1nAi2∑i=1nBi2\frac{A \cdot B}{||A|| ||B||} = \frac{\sum_{i=1}^{n}A_i B_i}{\sqrt{\sum_{i=1}^{n}A_i^2} \sqrt{\sum_{i=1}^{n}B_i^2}}

n개의 차원을 가지는 두 데이터 포인트 A(A1,A2,...,An)A(A_1, A_2, ..., A_n)와 B(B1,B2,...,Bn)B(B_1, B_2, ..., B_n)에 대한 코사인 유사도입니다.

계산 방법 - t-SNE 선택 시​

기울기(gradient) 계산 알고리즘을 선택합니다:

  • barnes_hut: 계산 복잡도가 낮아 큰 데이터셋에 적합합니다
  • exact: 계산 정확도가 높지만 계산 복잡도가 높아 큰 데이터셋에서는 시간이 오래 걸립니다

데이터 화이트닝 사용 여부 - PCA 선택 시​

PCA 기법에서 화이트닝(whitening)을 사용할지 선택합니다.

화이트닝은 인접한 feature들이 서로 덜 관련되도록(uncorrelated) 하고, 서로 같은 분산 값을 가지도록 하여 데이터들의 각 패턴을 독립적이고 비교 가능한 상태로 만듭니다.

사용 방법​

  1. 노드를 캔버스에 추가합니다
  2. 데이터셋을 입력 포트에 연결합니다
  3. 속성에서 사용하지 않을 열을 선택합니다 (필요한 경우)
  4. 차원 축소 방법을 선택합니다 (PCA 또는 t-SNE)
  5. 출력 차원 수를 설정합니다
  6. 선택한 방법에 따라 추가 파라미터를 설정합니다
    • t-SNE: 복잡도, 거리 측정 방법, 계산 방법
    • PCA: 데이터 화이트닝 사용 여부
  7. 노드를 실행하면 차원이 축소된 데이터셋이 출력됩니다

예제​

아이리스(Iris) 데이터셋을 2차원으로 축소하는 예제입니다.

원본 데이터는 꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비 등 4개의 차원을 가지고 있습니다.

PCA 예제​

PCA 예제

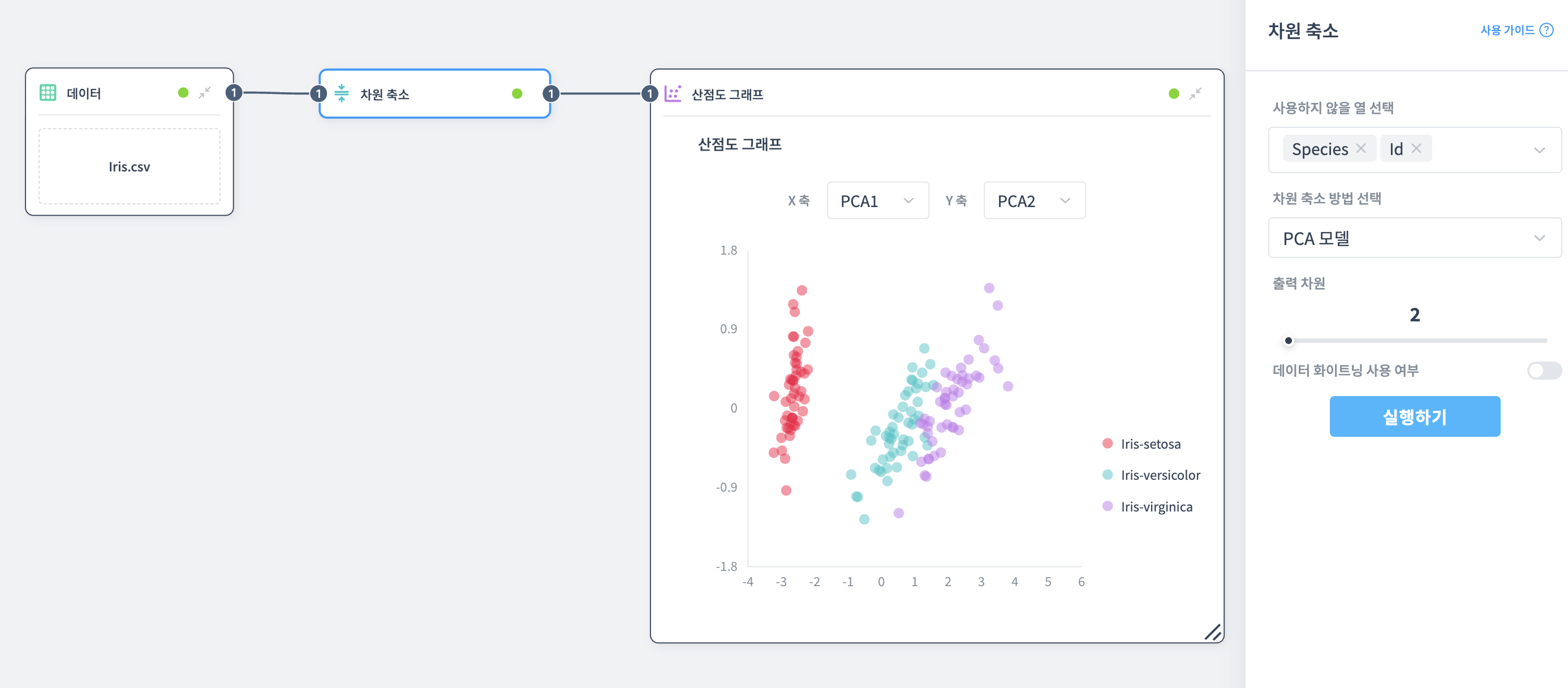
차원 축소 노드 속성 설정:

  • 사용하지 않을 열: Species, Id
  • 차원 축소 방법: PCA
  • 출력 차원: 2
  • 데이터 화이트닝: 비활성화

Scatter Plot 노드 속성 설정:

  • X축: PCA1
  • Y축: PCA2
  • 속성 열: Species (품종)

결과 해석:

PCA는 데이터의 분산을 최대한 보존하면서 차원을 축소합니다.

  • Setosa(빨강)는 왼쪽에 수직으로 길게 분포하며 다른 품종과 명확히 분리됩니다
  • Versicolor(하늘색)는 중앙에 위치합니다
  • Virginica(보라)는 오른쪽에 분포하며 Versicolor와 약간 겹치는 영역이 있습니다
  • PCA1 축(X축)이 품종 간 주요 차이를 나타내며, 세 품종이 좌측에서 우측으로 순서대로 배치됩니다

t-SNE 예제​

t-SNE 예제

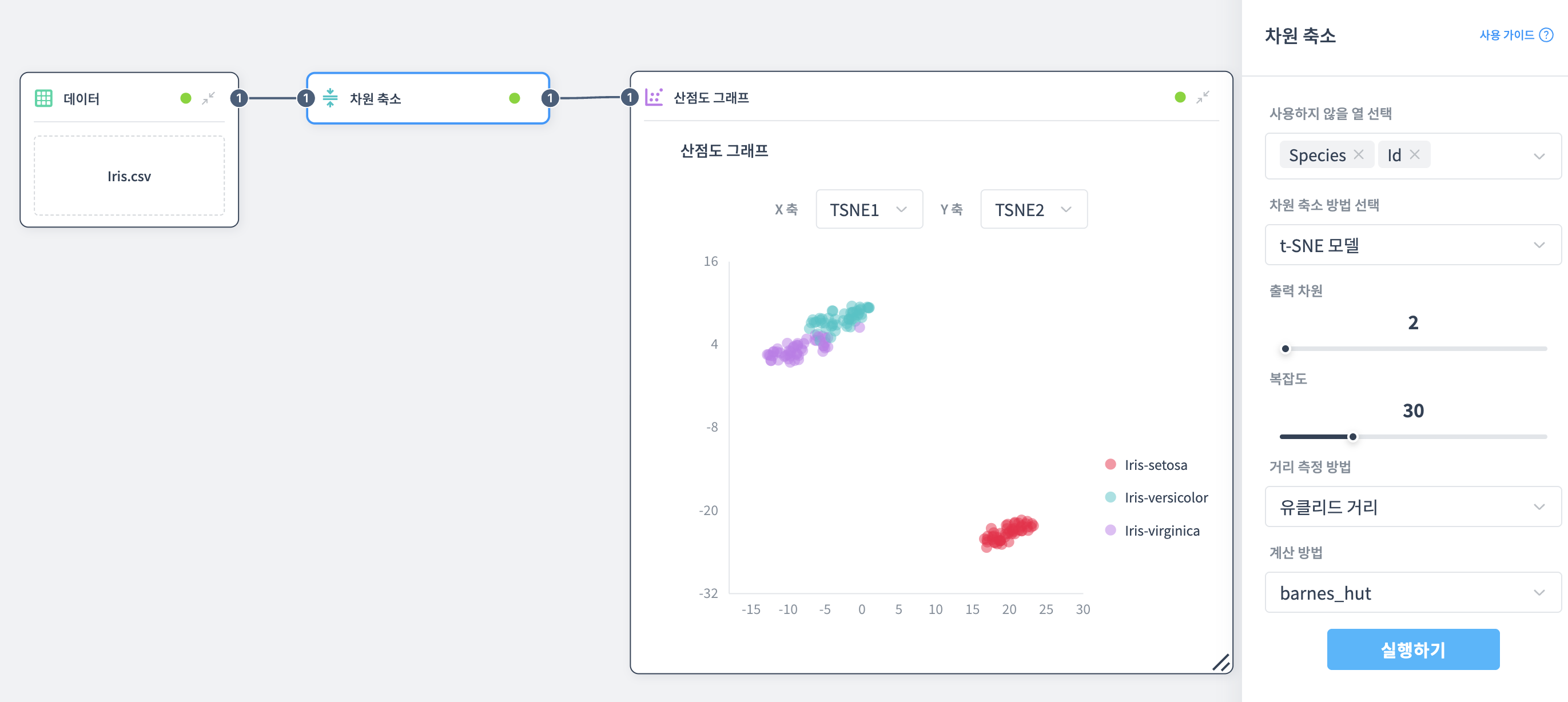
차원 축소 노드 속성 설정:

  • 사용하지 않을 열: Species, Id
  • 차원 축소 방법: t-SNE
  • 출력 차원: 2
  • 복잡도(Perplexity): 30
  • 거리 측정 방법: 유클리드 거리
  • 계산 방법: barnes_hut

Scatter Plot 노드 속성 설정:

  • X축: TSNE1
  • Y축: TSNE2
  • 속성 열: Species (품종)

결과 해석:

t-SNE는 데이터의 지역적 구조를 보존하면서 차원을 축소합니다.

  • Setosa(빨강)는 오른쪽 아래에 타이트한 클러스터를 형성하며 다른 품종과 완전히 분리됩니다
  • Versicolor(하늘색)와 Virginica(보라)는 왼쪽 위에서 인접한 두 개의 클러스터를 형성합니다
  • 각 클러스터 내에서 데이터가 PCA보다 더 밀집되어 있습니다
  • 세 품종이 명확하게 구분되는 덩어리로 표현되어 그룹 간 차이를 직관적으로 파악할 수 있습니다

PCA vs t-SNE:

  • PCA: 전체적인 데이터 구조와 분산을 유지, 계산이 빠름, 축에 의미가 있음
  • t-SNE: 지역적 클러스터 구조를 강조, 시각화에 유리, 파라미터 조정 필요

주의사항:

"사용하지 않을 열"에 Species와 Id를 선택해야 합니다:

  • Species: Scatter Plot에서 품종별로 색상을 구분하기 위해 필요합니다
  • Id: 단순 식별자이므로 차원 축소 계산에 포함하면 왜곡된 결과가 나올 수 있습니다